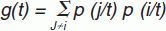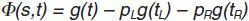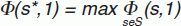Realizar una aproximación a la metodología de árboles de decisión tipo CART (Classification and Regression Trees) desarrollando un modelo para calcular la probabilidad de muerte hospitalaria en infarto agudo de miocardio (IAM).
MétodoSe utiliza el conjunto mínimo básico de datos al alta hospitalaria (CMBD) de Andalucía, Cataluña, Madrid y País Vasco de los años 2001 y 2002, que incluye los casos con IAM como diagnóstico principal. Los 33.203 pacientes se dividen aleatoriamente (70 y 30 %) en grupo de desarrollo (GD=23.277) y grupo de validación (GV=9.926). Como CART se utiliza un modelo inductivo basado en el algoritmo de Breiman, con análisis de sensibilidad mediante el índice de Gini y sistema de validación cruzada. Se compara con un modelo de regresión logística (RL) y una red neuronal artificial (RNA) (multilayer perceptron). Los modelos desarrollados se contrastan en el GV y sus propiedades se comparan con el área bajo la curva ROC (ABC) (intervalo de confianza del 95%).
ResultadosEn el GD el CART con ABC = 0,85 (0,86-0,88), RL 0,87 (0,86-0,88) y RNA 0,85 (0,85-0,86). En el GV el CART con ABC=0,85 (0,85-0,88), RL 0,86 (0,85-0,88) y RNA 0,84 (0,83-0,86).
ConclusionesLos 3 modelos obtienen resultados similares en su capacidad de discriminación. El modelo CART ofrece como ventaja su simplicidad de uso y de interpretación, ya que las reglas de decisión que generan pueden aplicarse sin necesidad de procesos matemáticos.
To provide an overview of decision trees based on CART (Classification and Regression Trees) methodology. As an example, we developed a CART model intended to estimate the probability of intrahospital death from acute myocardial infarction (AMI).
MethodWe employed the minimum data set (MDS) of Andalusia, Catalonia, Madrid and the Basque Country (2001-2002), which included 33,203 patients with a diagnosis of AMI. The 33,203 patients were randomly divided (70% and 30%) into the development (DS; n=23,277) and the validation (VS; n=9,926) sets. The CART inductive model was based on Breiman’s algorithm, with a sensitivity analysis based on the Gini index and cross-validation. We compared the results with those obtained by using both logistic regression (LR) and artificial neural network (ANN) (multilayer perceptron) models. The developed models were contrasted with the VS and their properties were evaluated with the area under the ROC curve (AUC) (95% confidence interval [CI]).
ResultsIn the DS, the CART showed an AUC=0.85 (0.86-0.88), LR 0.87 (0.86-0.88) and ANN 0.85 (0.85-0.86). In the VS, the CART showed an AUC = 0.85 (0.85-0.88), LR 0.86 (0.85-0.88) and ANN 0.84 (0.83-0.86).
ConclusionsNone of the methods tested outperformed the others in terms of discriminative ability. We found that the CART model was much easier to use and interpret, because the decision rules generated could be applied without the need for mathematical calculations.
En la toma de decisiones en medicina es importante buscar metodologías que sean precisas y nos ayuden a resolver los problemas que surgen a la hora de clasificar, estratificar o pronosticar a nuestros pacientes1.
Esta labor de clasificar adquiere más importancia si se dirige a crear directrices de planificación o en la elaboración de guías de actuación generales. A la hora de afrontar este problema de clasificación se han utilizado diversas aproximaciones metodológicas1.
Los distintos métodos empleados deben enfrentarse a 4 sucesivas barreras: a) seleccionar qué variables se utilizan como predictoras; b) analizar el tipo de variables y su naturaleza (p. ej., si siguen patrones de normalidad); c) valorar la posibilidad de interacciones entre las variables, y d) plantearse si el modelo resultante será útil en la práctica asistencial.
La utilización (en los últimos 10 años) de árboles de decisión, y entre ellos los de tipo CART (Classification and Regression Trees), aporta una aproximación que intenta solucionar estas 4 barreras y muestra, en algunas aplicaciones, ciertas ventajas respecto a otros modelos2. Su utilización se ha extendido a áreas de la biología y la medicina3-9.
Un árbol de clasificación es una forma de representar el conocimiento obtenido en el proceso de aprendizaje inductivo. Puede considerarse como la estructura resultante de la partición binaria recursiva del espacio de representación a partir del conjunto de registros utilizados. Cada registro está formado por el conjunto de valores de las variables predictoras y el valor de la variable resultado que corresponde a cada caso. Esta partición binaria recursiva se plasma en una organización jerárquica del espacio de representación que puede modelarse mediante una estructura tipo árbol. Cada nodo interior contiene una pregunta sobre una variable predictora concreta (con un hijo para cada una de las 2 posibles respuestas) y cada nodo hoja se refiere a un resultado (o clasificación)10.
Un esquema sencillo puede apreciarse en la figura 1. El problema es separar (clasificar) entre los 2 tipos de figuras (puntos y cruces) en el plano utilizando los valores de las 2 variables (X e Y). Se parte del nodo raíz con 20 puntos y 10 cruces. La primera pregunta es sobre la variable X (valores por encima de 3); si son valores por encima de 3 se constituye un nodo hoja (1) que clasifica correctamente 15 puntos. Si el valor de X no supera a 3 (tenemos 5 puntos y 10 cruces) y surge la segunda pregunta sobre la variable Y (por encima del valor 3), si son valores superiores a 3 en el nodo hoja (3) se clasifican 9 cruces y un punto. Si el valor de Y no supera a 3 se concluye en el nodo hoja (2) con 4 puntos y una cruz. Podríamos seguir haciendo particiones sucesivas hasta conseguir una clasificación pura. Naturalmente, en la mayoría de las ocasiones no se encuentra una clasificación absoluta o el árbol necesario para conseguirla es muy grande (podríamos llegar a un árbol con tantos nodos hojas como registros disponibles en nuestra base de datos).
La clasificación de patrones se realiza según una serie de preguntas sobre las variables predictoras, empezando por el nodo raíz (el primero o de origen) y siguiendo el camino determinado por las respuestas a las preguntas en los nodos internos, hasta llegar a un nodo hoja. La etiqueta asignada a este nodo hoja es la que determina la clasificación asignada.
La serie de preguntas/respuestas (que acaba en cada nodo hoja) constituye una regla de decisión.
Un árbol quedará resumido en el conjunto de reglas de decisión que lo compone. Para la interpretación de estas reglas se aplica un punto de vista lógico y la plausibilidad clínica. Puede decirse que la forma de pensar en medicina se aproxima a utilizar y sintetizar reglas de decisión que generalizan los problemas clínicos o diagnósticos; por ello, los árboles de decisión pueden ser bien aceptados por los médicos asistenciales.
El objetivo de este trabajo es acercarnos a la metodología CART, analizar un ejemplo (estratificar la mortalidad debida a un infarto agudo de miocardio [IAM] en pacientes ingresados), comparar con otras metodologías (regresión logística [RL] múltiple y red neuronal artificial [RNA]), según los resultados del ejemplo, y mostrar sus posibles ventajas y desventajas de forma general.
MétodoBase de datos. VariablesEstudio retrospectivo realizado con el conjunto mínimo básico de datos al alta hospitalaria (CMBD) de Andalucía, Cataluña, Madrid y País Vasco de los años 2001 y 2002, que incluye los casos con IAM como diagnóstico principal. Los datos de esta base (así como la definición de sus variables) ya se han descrito en otros trabajos11. Los 33.203 pacientes se dividen aleatoriamente (70-30%) en grupo de desarrollo (GD = 23.277) y grupo de validación (GV = 9.926). Utilizamos las 10 variables predictoras que mostraron más importancia en el análisis univariante (sexo, edad en años, hipertensión arterial [HTA], fibrilación ventricular [FV], arritmia, insuficiencia cardíaca, accidente cerebrovascular agudo [ACVA], insuficiencia respiratoria [IResp], insuficiencia renal [IRenal] y shock), y como variable de salida el estado (vivo/muerto) al alta hospitalaria.
Desarrollo de un árbol de clasificación (CART)El proceso pueden esquematizarse en 4 fases: construcción (building) del árbol, parada (stopping) del proceso de crecimiento del árbol (se constituye un árbol máximo que sobreajusta la información contenida en nuestra base de datos), podado (pruning) del árbol haciéndolo más sencillo y dejando sólo los nodos más importantes y, por último, selección (selection) del árbol óptimo con capacidad de generalización.
La construcción del árbol comienza en el nodo raíz, que incluye todos los registros de la base de datos. A partir de este nodo el programa debe buscar la variable más adecuada para partirlo en 2 nodos hijos. Para elegir la mejor variable debe utilizarse una medida de pureza (purity) en la valoración de los 2 nodos hijos posibles (la variable que consigue una mayor pureza se convierte en la utilizada en primer lugar, y así sucesivamente). Debe buscarse una función de partición (splitting function) que asegure que la pureza en los nodos hijos sea la máxima. Una de las funciones más utilizada es la denominada Gini (se alcanza un índice de pureza que se considera como máximo).
El índice de Gini en el nodo t, g(t), se puede formular del modo siguiente:
donde i y j son las categorías de la variable predictora y p es proporción.La función de criterio Φ(s,t) para la división s en el nodo t se define como:
donde pL es la proporción de casos de t enviados al nodo hijo de la izquierda, y pR al nodo hijo de la derecha.Cuando se comienza en el nodo raíz t = 1 (y también en las particiones sucesivas), se busca la división s*, de entre todas las posibles de S, que de un valor con mayor reducción de la impureza:
Luego se divide el nodo 1 en 2 nodos hijos (t = 2 y t = 3) utilizando la división s*. Este valor de la función de impureza, ponderado por la proporción de todos los casos del nodo t, es el valor del que se informa en el árbol como «mejora».
En el proceso sucesivo de construcción y crecimiento del árbol se debe asignar una clase (etiqueta) a cada nodo (desde la raíz hasta los nodos hoja). El procedimiento de asignación de clase debe hacerse por medio de una función de asignación, en la que se tiene en cuenta la probabilidad a priori asignada a cada clase (según la base de datos empleada), la pureza de la partición y la proporción final de casos que aparecen en los nodos hojas. Al igual que puede determinarse la pureza para un nodo concreto, puede evaluarse de forma conjunta para todo el árbol.
El crecimiento de un árbol continúa hasta que se produce cualquiera de estas 3 posibilidades: sólo hay una observación (caso) en cada nodo hoja, todas las observaciones tienen la misma probabilidad asignada en los nodos hoja (es imposible determinar el criterio de máxima pureza), o se ha fijado un límite externo de la profundidad (número de niveles máximo) del crecimiento del árbol. El árbol que se ha generado de esta forma clasifica correctamente los registros utilizados en su proceso de aprendizaje (se dice que este «sobrea-prendizaje» se obtiene porque el modelo ha «sobrea-justado» los datos empleados en esta fase), pero cuando se enfrente a nuevos registros no se asegura su capacidad de generalización.
El árbol complejo que se ha creado debe simplificarse para que alcance esta capacidad de generalización. Se utiliza un método de podado del árbol. El procedimiento asegura que sólo se retiran los nodos que incrementan muy poco la precisión del árbol. Se utiliza una medida de coste-complejidad (que combina los criterios de precisión frente a complejidad en el número de nodos y velocidad de procesamiento), buscando el árbol que obtiene menor valor en este parámetro. Los árboles más sencillos (podados con este criterio) aseguran una mayor capacidad de generalización.
De todos los árboles podados posibles debe seleccionarse el mejor. El mejor árbol (árbol solución) será el que consigue menor error en el ajuste de los registros utilizados en su proceso de aprendizaje. Pero esta condición no es suficiente, debe ajustar bien la base de datos utilizada en su aprendizaje, pero también debe ajustar registros no empleados en esta fase. Para conseguir este objetivo hay diversos métodos.
El método más común (implementado en los programas de mayor utilización), que no precisa un conjunto de prueba independiente, se denomina validación cruzada. La validación cruzada es un método de remuestreo que aprovecha el total de la información disponible en la base de datos sin prescindir de una parte de sus registros.
En la validación cruzada se divide de forma aleatoria la base de datos utilizada en la fase de aprendizaje (conjunto de aprendizaje) en N partes (normalmente 10). De forma secuencial, cada una de estos subconjuntos se reserva para emplearse como conjunto de prueba frente al modelo de árbol generado por los N-1 subconjuntos restantes. Obtenemos así N modelos diferentes, donde se puede evaluar la precisión de las clasificaciones tanto en el conjunto de aprendizaje (N-1) como en los subconjuntos de prueba (N), y podemos seleccionar el árbol óptimo cuando la precisión se alcance tanto en uno como en otro subconjunto.
Las diferencias principales entre los distintos algoritmos de construcción de árboles de decisión radican en las estrategias de poda y en la regla adoptada para partir los nodos.
Modelo de regresión logística múltiple y red neuronal artificialUtilizamos un modelo de RL con posibilidad de selección de variables por pasos.
Para el desarrollo de la RNA utilizamos una arquitectura de perceptrón multicapa (MLP, multilayered perceptron) entrenado con algoritmo de retropropagación del error (backpropagation). Este tipo de RNA es una de las más utilizadas en el ámbito de la medicina12.
Para la creación de la RNA utilizamos el programa comercial Qnet 97 (Vesta Services Inc.). Los parámetros de entrenamiento modificables en el software (momento, coeficiente de aprendizaje, etc.) fueron optimizados para alcanzar el mejor resultado de la red13.
Comparación de los modelosPara comparar los distintos modelos se medirán sus propiedades de sensibilidad (S), especificidad (E), área bajo la curva ROC (ABC) y porcentaje de correcta clasificación (PCC) con sus correspondientes intervalos de confianza (IC) del 95%14,15.
Utilizamos el test de Bland-Altman para comparar las probabilidades individuales obtenidas por cada modelo16.
Los cálculos estadísticos se realizaron con el programa SPSS 12.0.
ResultadoModelo de árbol de decisión CARTEl software que utilizamos (DTREG versión 3.5) utiliza de forma básica las características que hemos descrito en nuestra aproximación metodológica: modelo inductivo según el algoritmo de Breiman (forma de construcción del árbol), con análisis de sensibilidad basado en índice de Gini y sistema de validación cruzada.
Los otros parámetros utilizados (requeridos por el programa) fueron: control del tamaño del árbol (hoja con registros superiores a 15 y profundidad del árbol menor a 10), control del podado por reducción de error estándar, no selección del criterio de partición inicial y asignación de probabilidad de las categorías según la original de la base de datos.
Los resultados que se obtienen se muestran en las figuras 2 y 3. Como se puede apreciar, hay 2 subgrupos diferenciados según la variable sexo.
El árbol sólo ha utilizado 7 variables que, ordenadas según la importancia asignada, son: shock, edad, FV, insuficiencia cardíaca, sexo, ACVA e IRenal. El modelo se resume en 19 reglas de decisión (con las combinaciones de las 7 variables utilizadas).
Por ejemplo una de las reglas de decisión (fig. 2) es:
Si es hombre y no presenta shock, y si tiene menos de 68,5 años y FV, el modelo le asigna una probabilidad de mortalidad hospitalaria del 19,75%.
Simplemente observando los 2 árboles se detectan diferencias entre hombre y mujer. Los 2 árboles se pueden evaluar según aspectos clínicos y demuestran el diferente comportamiento entre hombres y mujeres (con mayor probabilidad de muerte a priori para las mujeres). También se observa el distinto peso de las variables (primero pregunta sobre la existencia de shock por su importancia en el pronóstico), para la edad el punto de corte diferente según sexo y, posteriormente, aparecen las otras variables que se consideran importantes. No hace falta realizar ningún cálculo para obtener la probabilidad asignada siguiendo cada la regla de decisión que nos lleva a cada nodo final.
Modelo de regresión logística múltipleEl resultado de la RL se muestra en la tabla 1. La variable arritmia quedó excluida en el análisis por pasos como no significativa. La tabla nos da información sobre la importancia de las variables (orden de los exponentes B), el grado de significación estadística y la posibilidad de cálculo de probabilidad asignada (por el modelo logístico) con los valores de los coeficientes beta por medio de su ecuación matemática.
Resultados del ajuste del modelo de regresión logística. Variable dependiente: mortalidad hospitalaria por infarto agudo de miocardio
| Variable | Coeficiente beta | DE | p | Exponente (B) | IC del 95% |
| Sexo (Mujer) | 0,176 | 0,057 | 0,002 | 1,192 | 1,067-1,332 |
| Edad (años) | 0,066 | 0,003 | 0,000 | 1,068 | 1,062-1,073 |
| HTA | 0,399 | 0,061 | 0,000 | 1,491 | 1,324-1,679 |
| FV | 2,074 | 0,090 | 0,000 | 7,956 | 6,664-9,499 |
| Insuficiencia cardíaca | 0,544 | 0,059 | 0,000 | 1,722 | 1,534-1,934 |
| ACVA | 1,921 | 0,145 | 0,000 | 6,828 | 5,143-9,066 |
| IResp | 1,209 | 0,109 | 0,000 | 3,351 | 2,708-4,148 |
| IRenal | 0,885 | 0,107 | 0,000 | 2,422 | 1,966-2,985 |
| Shock | 3,675 | 0,079 | 0,000 | 39,439 | 33,802-46,017 |
| Constante | −7,907 | 0,217 |
ACVA: accidente cerebrovascular agudo; DE: desviación estándar; FV: fibrilación ventricular; HTA: hipertensión arterial; IC: intervalo de confianza; IRenal: insuficiencia renal; IResp: insuficiencia respiratoria.
La arquitectura óptima para el modelo se seleccionó de forma empírica y consta de 3 capas (una de entrada, una oculta y una de salida). La capa de entrada con las 10 variables predictoras, la oculta con 4 nodos, y la de salida con un nodo que reflejaba la probabilidad de mortalidad hospitalaria, con redes más complejas no obtuvimos mejores resultados. La RNA, aun siendo sencilla, tiene un total de 44 parámetros (10 de la capa de entrada por 4 de la capa oculta más 4 de comunicación entre la capa oculta y el nodo de salida). El programa Qnet nos muestra el orden de importancia de las variables de entrada (que en este caso siguieron un patrón similar al conseguido por regresión logística que sólo utiliza 9 parámetros).
Comparación de los distintos modelosLos 3 modelos obtenidos con el GD se enfrentaron también al GV. El resumen de los resultados se expone en la tabla 2. Se aprecia que hay pocas diferencias entre los modelos en sus propiedades evaluadas. Se aprecia una menor sensibilidad en los modelos CART, pero recordamos que están trabajando con menos variables.
Comparación de la precisión de los 3 modelos de clasificación de probabilidad de mortalidad hospitalaria por infarto agudo de miocardio en los grupos de desarrollo (n = 23.277) y validación (n = 9.926)
| ABC (IC) | PCC (IC) | S (IC) | E (IC) | |
| Desarrollo | ||||
| RL | 0,87 (0,86-0,88) | 92 (91-92) | 76 (75-77) | 93 (92-93) |
| RNA | 0,85 (0,84-0,86) | 92 (91-92) | 76 (75-77) | 93 (92-93) |
| CART | 0,85 (0,85-0,86) | 92 (91-92) | 74 (73-75) | 93 (92-93) |
| Validación | ||||
| RL | 0,86 (0,85-0,88) | 92 (91-92) | 77 (76-78) | 93 (92-94) |
| RNA | 0,84 (0,83-0,86) | 92 (91-92) | 77 (76-78) | 93 (92-94) |
| CART | 0,85 (0,83-0,86) | 92 (91-92) | 73 (72-74) | 93 (92-94) |
ABC: área bajo la curva ROC; CART: modelo de árbol de clasificación tipo CART E: especificidad; IC: intervalo de confianza; PCC: porcentaje de correcta clasificación; RL: modelo de regresión logística; RNA: modelo de red neuronal artificial; S: sensibilidad.
En la figura 4 se muestran los gráficos de Bland-Altman obtenidos en el GD, y observamos que entre el modelo de RL y RNA hay menos diferencias (en las probabilidades de muerte hospitalaria individuales) que entre el modelo RL y el tipo CART (que muestra también la característica de ser discreto por sus 19 reglas de decisión). Atribuimos este resultado a que en este ejemplo todas las variables (menos la EDAD) son categóricas, por lo que el modelo RNA presenta más dificultades para encontrar interrelaciones entre las variables y así poder diferenciarse del modelo RL.
DiscusiónEn este ejemplo que hemos analizado, los resultados globales no diferencian (en la capacidad de discriminación) un modelo superior a otro, pero puede ser que en otras aplicaciones un modelo supere a los demás. El ejemplo también nos ha señalado que con las mismas variables predictoras los modelos son capaces de asignar, en algunos casos, probabilidades de muerte diferentes.
Las limitaciones que pueden argumentarse se centran en cada una de las metodologías empleadas: podríamos haber buscado interacciones entre las variables e incluirlas en el modelo de RL, utilizar otros tipos de RNA o arquitecturas más sofisticadas para conseguir mejores resultados con las redes, o aplicar otros algoritmos en el desarrollo de los árboles de decisión17. También podrían haberse empleado otras metodologías, como el análisis discriminante o la lógica fuzzy18,19.
En definitiva, con la misma información (mismas variables) pueden construirse distintas aproximaciones en un problema de clasificación. No hay una metodología que sea mejor en todos los casos, pero sí que expresan distintas capacidades que deben ser valoradas (tabla 3):
- –
Accesibilidad. Los paquetes estadísticos de uso habitual incluyen la RLM. Hay infinidad de publicaciones en medicina que emplean esta metodología. Los modelos basados en RNA y CART no son tan accesibles, ya que precisan programas específicos de menor difusión.
- –
Posibilidad de utilizar variables continuas o discretas. Los 3 modelos ofrecen esa posibilidad.
- –
Selección de variables según la importancia y la aportación de información. En RL y CART se hace de forma automática, y en RNA debe hacerse de forma «manual» (aunque hay otros programas que incorporan esta posibilidad).
- –
Modelo de asignación de probabilidad. El modelo RL es parámetrico (asignación según modelo logístico). El basado en CART es no paramétrico y las redes son el paradigma de aproximación universal de funciones.
- –
Interrelación de variables. En RL deben incluirse en el modelo, CART analiza las interrelaciones en sus reglas de decisión y en RNA pueden tenerse en cuenta todas las posibilidades.
- –
Interpretación de resultados. Aquí la ventaja está a favor del CART, es menor en RL y, en el caso de las RNA, son una caja negra en la interpretación de sus parámetros20.
Comparación de propiedades generales entre los modelos basados en regresión logística (RL), red neuronal artificial (RNA) y árbol de decisión tipo CART
| RL | RNA | CART | |
| Accesibilidad | ++ | − | − |
| Tipos de variables | ++ | ++ | ++ |
| Selección de variables | ++ | − | ++ |
| Importancia de variables | ++ | + | ++ |
| Interrelación de variables | + | +++ | ++ |
| Modelo | + | +++ | ++ |
| Interpretación de resultados | ++ | − | +++ |
Se ha graduado desde (−), peor, a (+++), mejor, las propiedades evaluadas.
Los modelos no son excluyentes: ante un mismo problema deben barajarse distintas metodologías que pueden colaborar en la búsqueda de un resultado óptimo21.
Como conclusión, podemos afirmar que los modelos basados en árboles de decisión ofrecen como ventaja una simplicidad en su utilización e interpretación ya que sus reglas de decisión no necesitan procesos matemáticos para ser interpretadas.
AgradecimientosEl presente trabajo ha contado con la financiación parcial de la Red Temática de Investigación Cooperativa de Investigación de Resultados y Servicios Sanitarios G03/202.