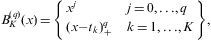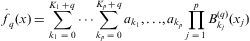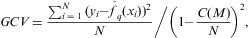Evaluar la eficiencia predictiva de modelos estadísticos paramétricos y no paramétricos para predecir episodios críticos de contaminación por material particulado PM10 del día siguiente, que superen en Santiago de Chile la norma de calidad diaria. Una predicción adecuada de tales episodios permite a la autoridad decretar medidas restrictivas que aminoren la gravedad del episodio, y consecuentemente proteger la salud de la comunidad.
MétodoSe trabajó con las concentraciones de material particulado PM10 registradas en una estación asociada a la red de monitorización de la calidad del aire MACAM-2, considerando 152 observaciones diarias de 14 variables, y con información meteorológica registrada durante los años 2001 a 2004. Se ajustaron modelos estadísticos paramétricos Gamma usando el paquete estadístico STATA v11, y no paramétricos usando una demo del software estadístico MARS v 2.0 distribuida por Salford-Systems.
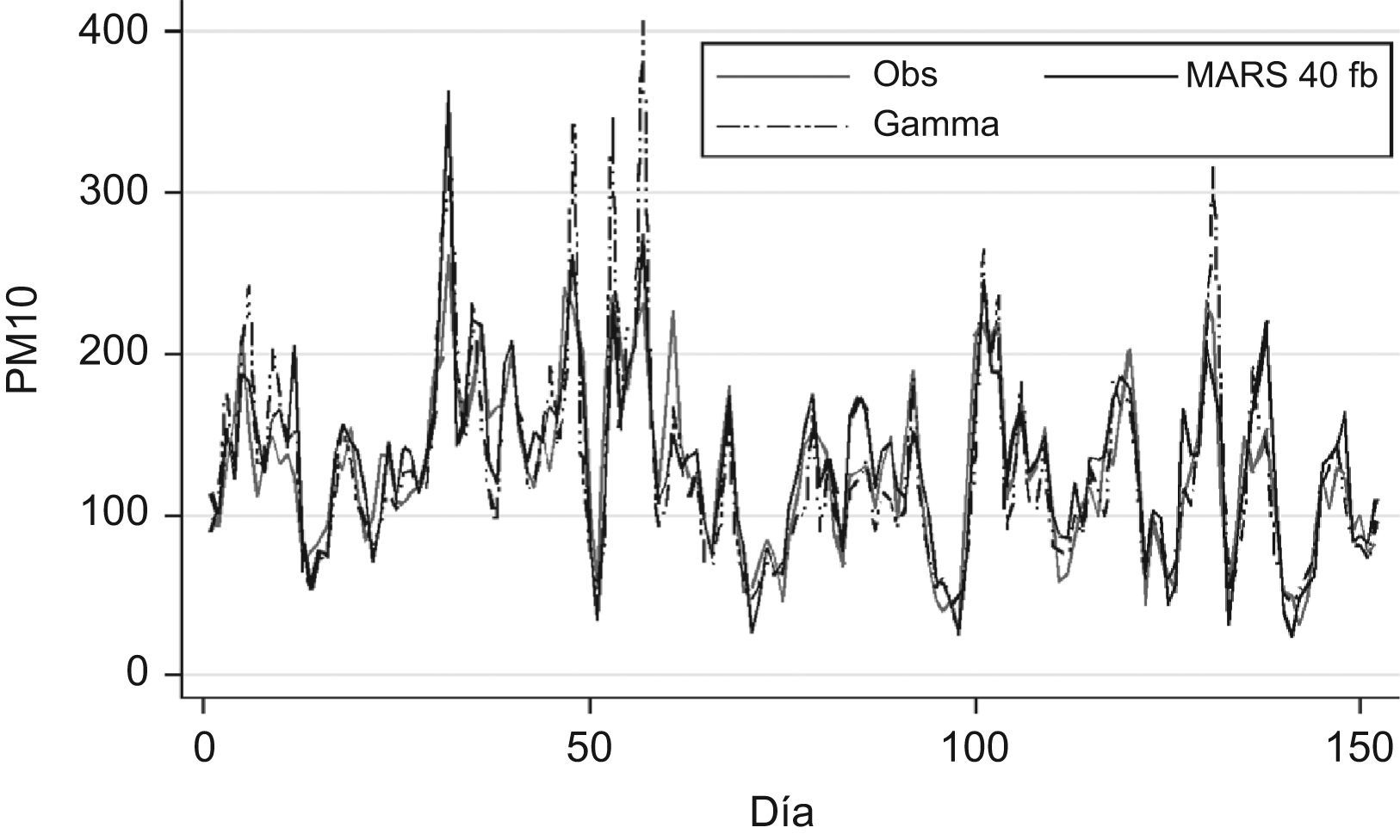
ResultadosAmbos métodos de modelación presentan una alta correlación entre los valores observados y los predichos. Los modelos Gamma presentan mejores aciertos que MARS para las concentraciones de PM10 con valores <240μg/m3 para el año 2001, y los modelos MARS presentan mejores aciertos para aquellas que exceden los 240μg/m3 de PM10 para todos los años.
ConclusionesLos modelos MARS son más eficientes para predecir episodios graves de alta contaminación por PM10 y posibilitan a la autoridad sanitaria adoptar restricciones preventivas que aminoren su efecto sobre la salud de la población. Esto se explicaría porque MARS corrige las variaciones de la serie a lo largo del tiempo, ajustando mejor la curva asociada a la concentración de PM10.
To evaluate the predictive efficiency of two statistical models (one parametric and the other non-parametric) to predict critical episodes of air pollution exceeding daily air quality standards in Santiago, Chile by using the next day PM10 maximum 24h value. Accurate prediction of such episodes would allow restrictive measures to be applied by health authorities to reduce their seriousness and protect the community’s health.
MethodsWe used the PM10 concentrations registered by a station of the Air Quality Monitoring Network (152 daily observations of 14 variables) and meteorological information gathered from 2001 to 2004. To construct predictive models, we fitted a parametric Gamma model using STATA v11 software and a non-parametric MARS model by using a demo version of Salford-Systems.
ResultsBoth models showed a high correlation between observed and predicted values. However, the Gamma model predicted PM10 values below 240μg/m3 more accurately than did MARS. The latter was more efficient in predicting PM10 values above 240μg/m3 throughout the study period.
ConclusionMARS models are more efficient in predicting extreme PM10 values and allow health authorities to adopt preventive methods to reduce the effects of these levels on the population’s health. The reason for this greater accuracy may be that MARS models correct variations in the series over time, thus better fitting the curve associated with PM10 concentrations.
Diversos estudios en todo el mundo han reportado los efectos de la contaminación del aire sobre la salud, especialmente la exposición a material particulado1–6. En la actualidad, el foco de la investigación son los efectos agudos y a corto plazo, especialmente sobre la mortalidad y la morbilidad por causas cardiovasculares y respiratorias7–11. Esto ha hecho que los países tomen una serie de medidas de gestión ambiental para controlar estas emisiones y, por otra parte, tratar de predecir tempranamente los episodios de alta contaminación del aire. Estas medidas han incluido un cambio sistemático a combustibles menos contaminantes, restricción diaria de la circulación a un determinado porcentaje de vehículos motorizados, cierre diario de algunas industrias, etc. Las causas que originan la contaminación son diversas, pero las actividades antropogénicas son las que más contribuyen al problema. Sin embargo, el grado de contaminación también está influenciado por otros factores, como el clima y la topografía. El clima influye de manera decisiva en la persistencia de los contaminantes atmosféricos; el viento, la temperatura y la radiación solar modifican de manera drástica la dispersión y el tipo de contaminantes que puede haber en un determinado momento; la topografía influye en el movimiento de las masas de aire y por lo tanto en la persistencia de la contaminación en una determinada zona geográfica. La combinación de todos estos factores determina finalmente la calidad del aire5.
La predicción de los episodios graves de contaminación del aire en las grandes ciudades se ha transformado en una herramienta de gestión ambiental orientada a proteger la salud de la población, que permite a la autoridad sanitaria conocer, con cierta certeza, el probable grado de contaminación atmosférica que habrá en un determinado lapso de tiempo. Esta predicción se ha abordado mediante diversos modelos, combinando aproximaciones determinísticas y probabilísticas e incorporando diversos tipos de información12–17. La metodología actual y oficial de la Región Metropolitana de Santiago de Chile respecto al pronóstico de las concentraciones de material particulado PM10 se realiza con el Modelo Cassmassi, propuesto en 1999 por Joseph Cassmassi18, que aplica una regresión lineal múltiple y pronostica el valor máximo de la concentración promedio de 24h de PM10 para el período de las 00h a las 24h del día siguiente. Este modelo incluye variables meteorológicas observadas, índices de condiciones meteorológicas observadas y pronosticadas, concentraciones de contaminantes observadas, índices de variaciones esperadas de emisiones y otros.
Para las concentraciones de PM10 se han usado en Chile diferentes métodos estadísticos para modelar concentraciones de contaminantes del aire, incluyendo series de tiempo19, redes neuronales20,21 y modelos de regresión adaptativos basados en funciones de suavizamiento (spline) llamadas Multivariate Adaptive Regression Splines (MARS)22. La eficiencia predictiva de estos modelos es variable y está estrechamente asociada al comportamiento y la evolución de los determinantes ambientales. Los modelos que utilizan la teoría de los valores extremos están siendo ampliamente usados para este fin, en especial en aquellos episodios que ocurren en periodos cortos de tiempo y presentan valores extremos o excedencias de los valores límite de alerta o emergencia establecidos por la autoridad23,24.
El objetivo de este trabajo es comparar la eficiencia predictiva de los modelos multivariados Gamma y MARS para pronosticar el máximo de concentración de PM10 del día siguiente en Santiago de Chile en el periodo comprendido entre el 1 de abril y el 31 de agosto de los años 2001, 2002, 2003 y 2004.
MétodosFuentes de informaciónSe utilizaron las bases de datos de PM10 de la estación de monitorización Pudahuel de la red MACAM2-RM, de los años 2001, 2002, 2003 y 2004. Para cada año estudiado se seleccionaron las mediciones entre el 1 de abril y el 31 de agosto, que corresponde a la época del año con menor ventilación en la cuenca de Santiago. Se trabajó con el promedio móvil de 24h. En caso de faltar datos, éstos se imputaron por los generados mediante un suavizamiento doble exponencial con un valor de coeficiente de suavización α=0.70 (Anexo 1). Se trabajó con esta estación porque la mayor parte del año presenta los mayores índices de concentración de PM10. Además, es la que tiene mayor influencia en la toma de decisiones administrativas respecto a pronósticos de episodios graves del día siguiente. Por otra parte, producto de las medidas de gestión ambiental implementadas en el momento de declarar episodios graves de contaminación por PM10, se afecta el comportamiento de la serie de tiempo, generando valores de concentraciones menores que no reflejan la concentración real observada, por lo que penalizamos este efecto mediante una constante de corrección. En la práctica, esta constante viene dada por ΔCI=media[CPM24I−1−CPM24I], en donde CPM24I−1yCPM24I corresponden a los promedios de concentración de PM10 el día antes y el día de la intervención, respectivamente, para cada mes del año del periodo de estudio. La distribución del número de episodios observados que superan los 240μg/m3 para los años 2001, 2002, 2003 y 2004 corresponde a 4 (2,6%), 11 (7,2%), 5 (3,3%) y 2 (1,3%), respectivamente25.
ProcedimientosSe usaron 152 observaciones multidimensionales compuestas por una variable respuesta PM10 y 13 variables predictoras. La modelación contempla retrasos de 1 y 2 días respecto a las variables de interés del día de mañana (N+1), que corresponde al día a modelar. Las variables predictoras del día de hoy (retraso de 1 día) se definieron como: promedio horario de concentración PM10 a las 0:00h del día N (pm0), promedio horario de concentración PM10 a las 6:00h del día N (pm6), promedio horario de concentración PM10 a las 12:00h del día N (pm12) y promedio horario de concentración PM10 a las 18:00h del día N (pm18). Las variables predictoras que incorporan retrasos de 2 días (N−1) son: máximo de concentración del promedio móvil 24h de PM10 entre las 19:00h del día N−1 y las 18:00h del día N (pm10h), máxima temperatura entre las 19:00h del día N−1 y las 18:00h del día N (mth), mínima humedad relativa entre las 19:00h del día N−1 y las 18:00h del día N (mhrh), temperatura máxima menos mínima entre las 19:00h del día N−1 y las 18:00h del día N (dth), y promedio de la velocidad del viento entre las 19:00h del día N−1 y las 18:00h del día N (vvh). Las variables predictoras del día de mañana (N+1) corresponden a: máxima temperatura del día N+1 (mtm), mínima humedad relativa del día N+1 (mhrm), temperatura máxima menos mínima del día N+1 (dtm) y promedio de la velocidad del viento del día N+1 (vvm). La respuesta en estudio es el máximo de concentración del promedio móvil de 24h de PM10 del día N+1 (pm10m). Los valores de las variables del día de mañana son pronósticos validados y entregados por la Dirección Meteorológica de Chile usando un modelo Mesoscale Modeling System (MM5), un modelo numérico que utiliza las ecuaciones de la física de la atmósfera para la predicción meteorológica en áreas limitadas26.
Las autoridades de la Comisión Nacional del Medio Ambiente (CONAMA) han definido cuatro grados de concentraciones de PM10 con el fin de tomar decisiones administrativas en el momento de producirse episodios graves: bueno, 0–193μg/m3; alerta, 194–239μg/m3; preemergencia, 240–329μg/m3; y emergencia, >330μg/m322. Para nuestro estudio dicotomizamos la respuesta en dos clases: 1) pm10m <240μg/m3 y 2) pm10m >240μg/m3; es decir, «bueno o alerta» frente a «preemergencia o emergencia». El objetivo de la dicotomización es poder generar tabulaciones cruzadas entre los valores observados de la variable respuesta y las predicciones, para poder evaluar la proporción de aciertos a las dos clases por parte de los modelos propuestos.
Construcción de los modelos Gamma y MARSEl ajuste de los modelos de un determinado año se validó con la información del año inmediatamente posterior; con ello se garantiza la independencia de los datos usados para su validación respecto a los usados en su construcción. Por tal motivo no se entregan predicciones para el modelo del año construido con información del año 2004, pues no se posee información del año 2005. Cada modelo fue estimado con los datos del periodo comprendido entre el 1 de abril y el 31 de agosto de un año, y se aplicó a los datos del año siguiente, para el mismo periodo, evaluando el ajuste de esas estimaciones en contraste con las observaciones reales correspondientes al segundo año. Ambos modelos se describen con detalle en el Anexo 2.
Regresión GammaLos modelos Gamma se usan en situaciones en que la variable posee valores mayores o iguales a cero. Originalmente se utilizaron para datos continuos, pero en la actualidad la familia de modelos lineales generalizados Gamma se utiliza para datos de recuento27. En general, estos modelos consideran distintas maneras de cómo trabajar la variable respuesta, por ejemplo la exponenciación de la respuesta usando la transformación log-gamma28.
Regresión Adaptativa Multivariada (MARS)MARS es una metodología propuesta por Friedman29 en el año 1991, que intenta construir un modelo de regresión no lineal basado en un producto de funciones llamado «base de suavizamiento» (spline). Estas funciones incorporan en su estructura los predictores, que entran en la modelación como parte de una función y no directamente como en la regresión clásica, y producen un modelo para la respuesta en estudio, que puede ser de tipo continua o binaria, que automáticamente selecciona las variables predictoras que aparecen en la ecuación final, las que se incorporan en las funciones llamadas «base de suavizamiento»30,32.
En nuestro estudio, con el objetivo de comparar los modelos se consideraron los siguientes estadísticos: a) correlación lineal de Pearson entre el valor observado y el predicho, y b) proporción de error medio absoluto (mpab) entre el valor observado (obs) y el valor predicho (pred), dado por mpab=∑i=1n{[|(PM10obs−PM10pred)|/(PM10obs)]}/n, que equivale a evaluar los errores promedio cometidos por ambos modelos en las predicciones. Además, se consideró la proporción de aciertos en cada clase.
Se construyeron dos modelos MARS por año, uno con 20 funciones base y otro con 40, con el fin de comparar los ajustes de los modelos y las regiones seleccionadas para la predicción de la variable respuesta, lo que permite elegir el modelo que mejor ajusta la respuesta esperada incorporando particiones en el dominio de las variables predictoras32. En el caso de la regresión Gamma se trabajó usando la función de enlace logaritmo, con tres conjuntos de variables predictoras: el primero corresponde a todas las variables, el segundo sólo a variables de ayer y hoy, y el tercero a las variables pm0, pm6, pm18, dtm, dth y vvm. Este último conjunto explicaría mejor el comportamiento de las concentraciones de la variable respuesta, tal como ya han descrito otros autores20.
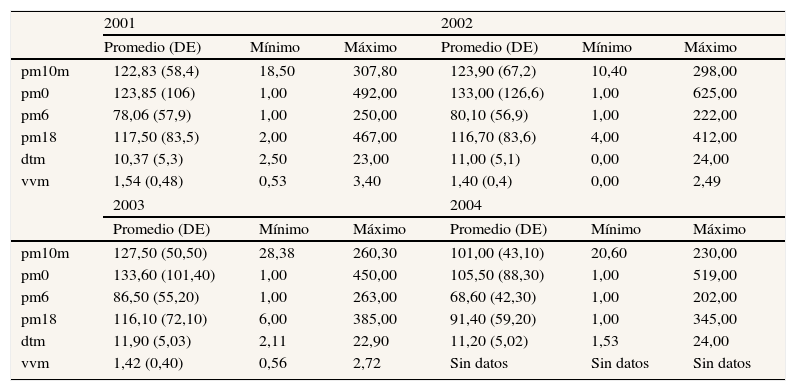
ResultadosLa tabla 1 muestra los estadísticos descriptivos de las variables incorporadas a la modelación final de concentraciones de PM10. Se puede ver que los máximos para los años 2001, 2002 y 2003 exceden el valor de 240μg/m3; para el año 2004 no se aprecia tal comportamiento.
Medidas de posición y dispersión variables utilizadas en modelación de PM10
| 2001 | 2002 | |||||
| Promedio (DE) | Mínimo | Máximo | Promedio (DE) | Mínimo | Máximo | |
| pm10m | 122,83 (58,4) | 18,50 | 307,80 | 123,90 (67,2) | 10,40 | 298,00 |
| pm0 | 123,85 (106) | 1,00 | 492,00 | 133,00 (126,6) | 1,00 | 625,00 |
| pm6 | 78,06 (57,9) | 1,00 | 250,00 | 80,10 (56,9) | 1,00 | 222,00 |
| pm18 | 117,50 (83,5) | 2,00 | 467,00 | 116,70 (83,6) | 4,00 | 412,00 |
| dtm | 10,37 (5,3) | 2,50 | 23,00 | 11,00 (5,1) | 0,00 | 24,00 |
| vvm | 1,54 (0,48) | 0,53 | 3,40 | 1,40 (0,4) | 0,00 | 2,49 |
| 2003 | 2004 | |||||
| Promedio (DE) | Mínimo | Máximo | Promedio (DE) | Mínimo | Máximo | |
| pm10m | 127,50 (50,50) | 28,38 | 260,30 | 101,00 (43,10) | 20,60 | 230,00 |
| pm0 | 133,60 (101,40) | 1,00 | 450,00 | 105,50 (88,30) | 1,00 | 519,00 |
| pm6 | 86,50 (55,20) | 1,00 | 263,00 | 68,60 (42,30) | 1,00 | 202,00 |
| pm18 | 116,10 (72,10) | 6,00 | 385,00 | 91,40 (59,20) | 1,00 | 345,00 |
| dtm | 11,90 (5,03) | 2,11 | 22,90 | 11,20 (5,02) | 1,53 | 24,00 |
| vvm | 1,42 (0,40) | 0,56 | 2,72 | Sin datos | Sin datos | Sin datos |
DE: desviación estándar; dtm: diferencia de temperatura del día de mañana; pm0, 6, 18: concentración de material particulado PM10 de la hora 0 del día anterior, de la hora 6 del día anterior y de la hora 18 del día anterior, respectivamente; pm10m: máximo de concentración de PM10 del día de mañana; vvm: velocidad del viento del día de mañana.
La tabla 2 muestra los aciertos a la clase i y ii por parte de los modelos Gamma y los aciertos a ambas clases por los modelos MARS. Las correlaciones son significativas para los tres tipos de modelo por año, pero los mpab se mantienen altos para todos los modelos salvo el de 40 funciones base de MARS del año 2002, en el cual se aprecia un 19% de error medio absoluto, al igual que en el modelo Gamma. En general, para los 3 años los modelos Gamma presentan mejores aciertos que MARS para las concentraciones de PM10 con valores <240μg/m3, y los modelos MARS presentan mejores aciertos para aquellas que exceden los 240μg/m3 de PM10.
Resultados de modelación MARS y Gamma
| 2001 a 2002 | 2002 a 2003 | 2003 a 2004 | |||||||
| Gamma | MARS 20 fb | MARS 40 fb | Gamma | MARS 20 fb | MARS 40 fb | Gamma | MARS 20 fb | MARS 40 fb | |
| mpab (%) | 38,00 | 39,00 | 32,00 | 19,00 | 29,00 | 19,00 | 28,00 | 25,00 | 25,00 |
| rpearson | 0,83 | 0,88 | 0,74 | 0,82 | 0,81 | 0,86 | 0,78 | 0,82 | 0,82 |
| Clase I (%) | 98,00 | 67,00 | 44,40 | 99,00 | 0,00 | 100,00 | 99,00 | 100,00 | 99,00 |
| Clase II (%) | 50,00 | 99,30 | 95,40 | 12,50 | 98,00 | 97,00 | 0,00 | 0,00 | 0,00 |
fb: funciones base; mpab: proporción de error medio absoluto.
La figura 1 muestra que las predicciones del modelo Gamma para altas concentraciones de PM10 se aleja más que lo predicho por MARS, pero para valores<200μg/m3 el modelo Gamma proporciona mejores predicciones.
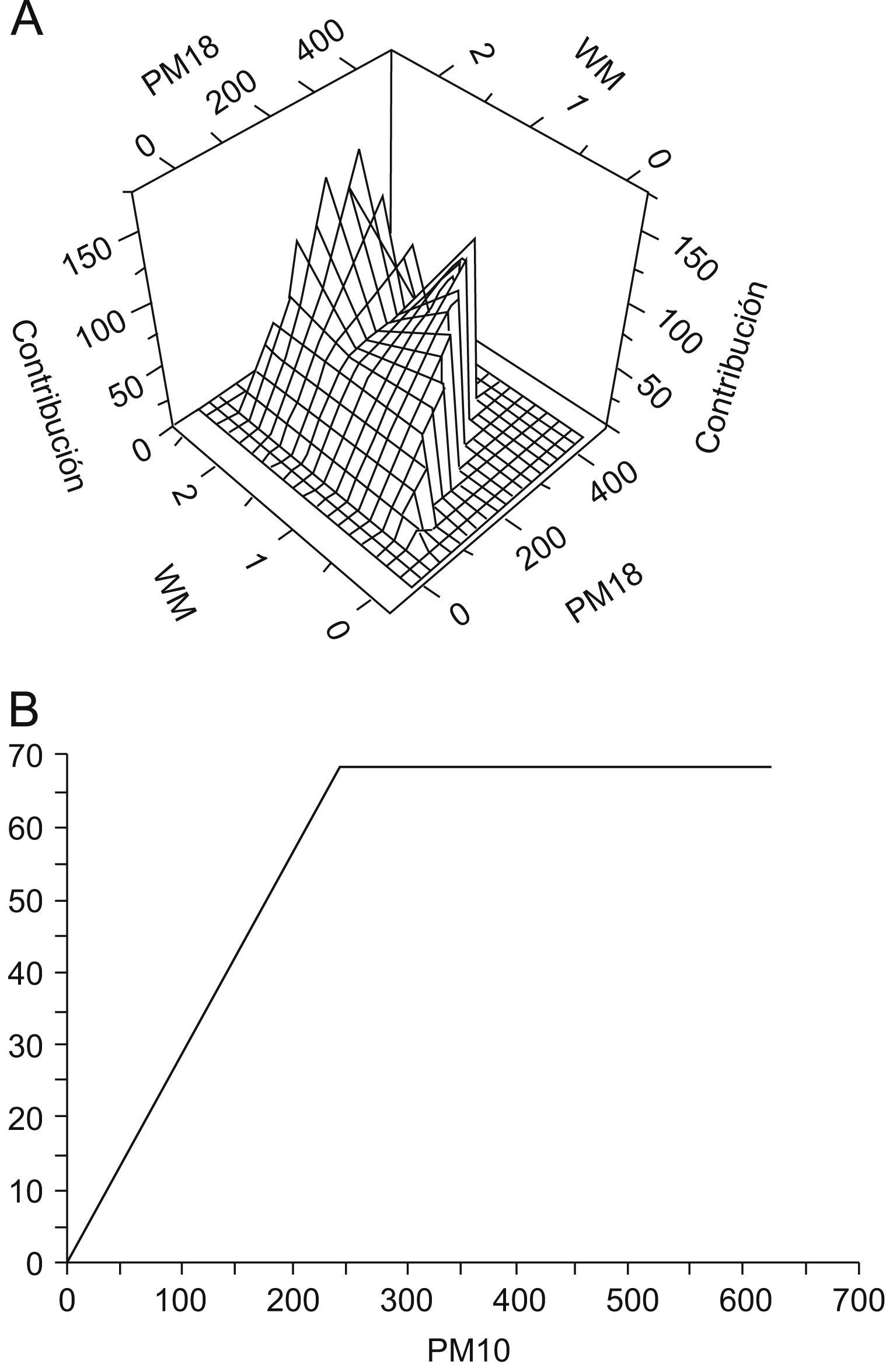
La figura 2, del modelo MARS de 40 funciones base del año 2002, muestra las relaciones de las interacciones de la función base max(0; pm18-137) y max(0; vvm-1,522) que generan la función base BF8, la cual representa una superficie de interacción (tabla 3) cuyo máximo alcanza 165μg/m3. Esto indica que con valores superiores a 137μg/m3 en las concentraciones de PM10 a las 18:00h (pm18) y >1,522m/s en la velocidad del viento del día de mañana, el aporte a la concentración de PM10 del día de mañana por parte de la interacción se hace máximo en 165μg/m3. Por su parte, también se observa que en la variable pm0 con concentraciones por encima de 240μg/m3 el aporte máximo a la respuesta es de aproximadamente 70μg/m3, lo cual representa el valor con el cual la función base BF4 contribuiría a la respuesta.
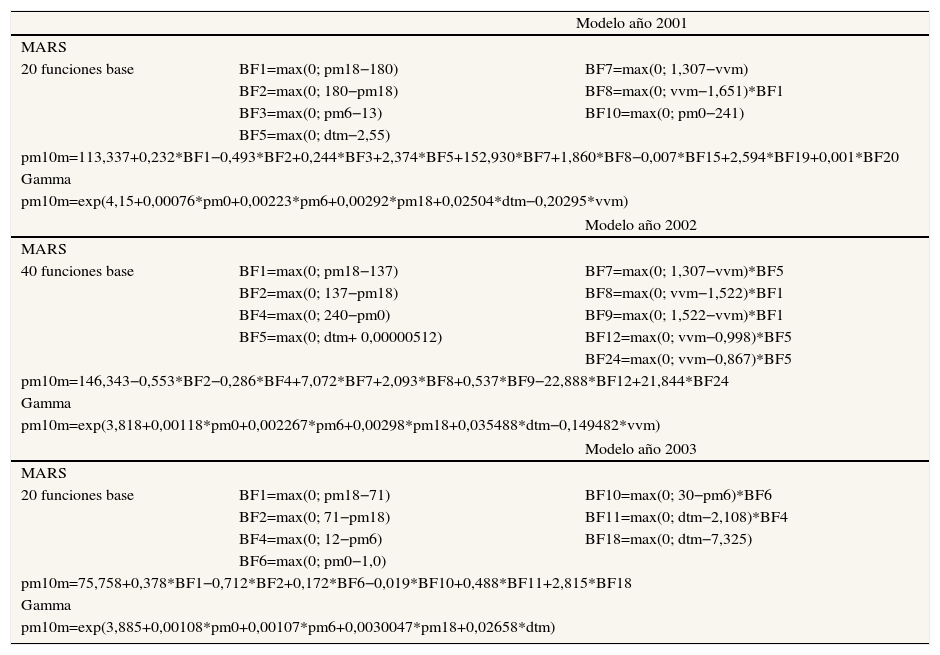
Modelos explícitos para MARS de 20 y 40 funciones base y Gamma para los años 2001, 2002 y 2003
| Modelo año 2001 | ||
| MARS | ||
| 20 funciones base | BF1=max(0; pm18−180) | BF7=max(0; 1,307−vvm) |
| BF2=max(0; 180−pm18) | BF8=max(0; vvm−1,651)*BF1 | |
| BF3=max(0; pm6−13) | BF10=max(0; pm0−241) | |
| BF5=max(0; dtm−2,55) | ||
| pm10m=113,337+0,232*BF1−0,493*BF2+0,244*BF3+2,374*BF5+152,930*BF7+1,860*BF8−0,007*BF15+2,594*BF19+0,001*BF20 | ||
| Gamma | ||
| pm10m=exp(4,15+0,00076*pm0+0,00223*pm6+0,00292*pm18+0,02504*dtm−0,20295*vvm) | ||
| Modelo año 2002 | ||
| MARS | ||
| 40 funciones base | BF1=max(0; pm18−137) | BF7=max(0; 1,307−vvm)*BF5 |
| BF2=max(0; 137−pm18) | BF8=max(0; vvm−1,522)*BF1 | |
| BF4=max(0; 240−pm0) | BF9=max(0; 1,522−vvm)*BF1 | |
| BF5=max(0; dtm+ 0,00000512) | BF12=max(0; vvm−0,998)*BF5 | |
| BF24=max(0; vvm−0,867)*BF5 | ||
| pm10m=146,343−0,553*BF2−0,286*BF4+7,072*BF7+2,093*BF8+0,537*BF9−22,888*BF12+21,844*BF24 | ||
| Gamma | ||
| pm10m=exp(3,818+0,00118*pm0+0,002267*pm6+0,00298*pm18+0,035488*dtm−0,149482*vvm) | ||
| Modelo año 2003 | ||
| MARS | ||
| 20 funciones base | BF1=max(0; pm18−71) | BF10=max(0; 30−pm6)*BF6 |
| BF2=max(0; 71−pm18) | BF11=max(0; dtm−2,108)*BF4 | |
| BF4=max(0; 12−pm6) | BF18=max(0; dtm−7,325) | |
| BF6=max(0; pm0−1,0) | ||
| pm10m=75,758+0,378*BF1−0,712*BF2+0,172*BF6−0,019*BF10+0,488*BF11+2,815*BF18 | ||
| Gamma | ||
| pm10m=exp(3,885+0,00108*pm0+0,00107*pm6+0,0030047*pm18+0,02658*dtm) | ||
BF: funciones base; dtm: diferencia de temperatura del día de mañana; pm0, 6, 18: concentración de material particulado PM10 de la hora 0 del día anterior, de la hora 6 del día anterior y de la hora 18 del día anterior, respectivamente; pm10m: máximo de concentración de PM10 del día de mañana; vvm: velocidad del viento del día de mañana.
La tabla 3 muestra los modelos explícitos para los modelos MARS de 20 y 40 funciones base y los modelos Gamma para los años 2001, 2002 y 2003. La complejidad del modelo se aprecia en el número de funciones base incorporadas al modelo explícito; en este caso, el modelo del año 2002 posee nueve funciones base, de las cuales cinco corresponden a interacciones de funciones base univariadas, las funciones BF8 y BF9 corresponden a las interacciones de las funciones espejo respecto a la variable vvm y la correspondiente función base asociada a la variable pm18.
DiscusiónLa modelación MARS selecciona aquellas variables predictoras significativas y detecta posibles interacciones de ellas, generando modelos más flexibles desde el punto de vista de la interpretación. Ya que las interacciones siempre están restringidas a alguna subregión, éstas quedan expresadas algebraicamente mediante las funciones base, logrando de esta forma establecer un modelo parsimonioso que representa sin ningún tipo de transformación adicional la naturaleza propia de las variables que se están trabajando. Crea nodos o puntos de corte que actúan como valores umbral para cada variable predictora seleccionada, indicando el cambio que se genera en la contribución por parte de la función base a la respuesta en estudio.
Una vez seleccionado el modelo óptimo, MARS ajusta nuevamente el modelo para cada variable, de modo de determinar el impacto en la calidad del modelo al eliminar dicha variable; así se asigna un ranking relativo desde la variable más importante a la menos importante. De esta manera se definen variables de reemplazo o competidoras, con lo cual la metodología MARS permite tratar los valores perdidos o faltantes generando una función base exclusiva para aquellas variables que no poseen información, es decir, se genera una función base de imputación cuya finalidad es imputar el valor promedio de la variable predictora sin información.
Tal y como se ha podido determinar en el presente estudio, los modelos MARS resultaron similares en su eficiencia predictiva al cambiar el número de funciones base, independientemente del año para el cual se construyó el modelo y del año con que se validó. Partir el espacio asociado al rango de las variables predictoras no mejoró la calidad de las predicciones, y en ocasiones se vio que con una partición menos fina (menos subregiones) la metodología era más robusta que con una partición más fina. Esto podría explicarse por el hecho de que con el tiempo las series de PM10 muestran una tendencia descendente y variaciones en las concentraciones más bajas, por las medidas de intervención aplicadas33.
En el caso de la estación de monitorización Pudahuel, ésta presentó cambios en las concentraciones anuales y mensuales de material particulado PM10 entre los años 1998 y 2004, básicamente debidos a la implementación de medidas de descontaminación global y de medidas extraordinarias los días de episodios graves, al uso del modelo de pronóstico de episodios graves y a los factores meteorológicos. Tales cambios influyen en el funcionamiento de los modelos y hacen que éstos no sean tan complejos en su estructura, puesto que la relación que se establece entre las variables predictoras no es tan complicada y ello se refleja en las funciones base construidas. A su vez, se observan diferencias de un año a otro, lo que podría estar influenciado por las condiciones meteorológicas particulares de cada año (año seco, fenómeno del niño u otros cambios climáticos). Otro factor a evaluar y que podría ser relevante es el aumento del parque automotriz en los últimos años.
Adicionalmente se han implementado diferentes métodos para modelar la concentración de material particulado en la región metropolitana de Santiago de Chile. Por ejemplo, Silva et al19, aplicando series de tiempo utilizando funciones de transferencia involucrando variables meteorológicas, describieron un 40% de proporción media de error absoluto en la predicción de los episodios críticos. Por otra parte, Pérez et al21, usando redes neuronales con suavizamiento previo, hallaron aproximadamente un 30% de error medio absoluto en la predicción de los episodios graves21. Otros trabajos del mismo autor usando redes neuronales muestran mejores resultados que con una una regresión lineal clásica20. Por otra parte, Silva et al22 evaluaron dos aproximaciones metodológicas al problema de la predicción de la contaminación del aire por material particulado, y observaron que MARS proporcionó mejores predicciones que el análisis discriminante.
En el caso de las aplicaciones de los modelos a la estación de monitorización Pudahuel, las variables predictoras que mejor explican la respuesta serían las concentraciones concretas de PM10 (pm0, pm6 y pm18) y las variables meteorológicas (dtm y vvm), lo cual concuerda en el sentido de que MARS selecciona adecuadamente variables relacionadas con la persistencia de las condiciones de ventilación, las que tienen relación con la meteorología22.
Los métodos de predicción aplicados nos proporcionan modelos adecuados para estudiar la contaminación por material particulado. En general, la regresión Gamma fue inferior que MARS en cuanto a aciertos de la clase ii, salvo en el modelo del año 2003 que predice para el año 2004, en el cual los aciertos en la clase ii no fueron efectivos, por lo que MARS se presenta como una mejor herramienta de predicción de episodios de contaminación por encima de 240μg/m3. Por otra parte, una ventaja del modelo Gamma es que en general hace mejores predicciones para la clase i (concentraciones de PM10 <240μg/m3); es decir, es sensible a valores de concentraciones de material particulado que decretan calidad del aire buena o alerta, y ello vendría dado por el comportamiento de la variable de interés. Por ejemplo, para el año 2001, el producto de las medidas de intervención hace que la modelación Gamma ajuste mejor en ese año, ya que para años posteriores estas medidas han tenido un impacto moderado en los valores de la serie de PM10, haciendo menos eficientes estos modelos frente a los MARS, como acontece para los años 2002, 2003 y 2004.
Este trabajo básicamente apunta a que las modelaciones propuestas permitan detectar concentraciones por encima del valor umbral de 240μg/m3, que es el que decreta la alerta epidemiológica en Santiago de Chile. Esta consideración haría de la modelación MARS una herramienta de mayor poder estadístico en comparación con un modelo de tipo Gamma. Este último punto concuerda con los resultados de otros autores, que muestran que MARS es más eficiente que otras técnicas22,34,35. Esto podría explicarse por la aproximación de suavizamiento que usa esta metodología, que genera quiebres en la serie de tiempo de los predictores y ajusta localmente las funciones base en función de dichos quiebres o nodos.
FinanciaciónNIH/Fogarty Grant #D43TW 05746-02.
Contribuciones de autoríaS.A. Alvarado concibió el estudio y obtuvo la financiación, desarrolló los análisis estadísticos, redactó los apartados de métodos, resultados y discusión, y elaboró las gráficas. C.S. Silva preparó los datos primarios y los llevó al formato a usar para la modelación, redactó la parte de métodos junto al primer autor y ayudó en la redacción de la discusión. D.D. Cáceres escribió la introducción, revisó y colaboró en los análisis estadísticos y la edición de las tablas, y ayudó en la redacción de la discusión. S.A. Alvarado es el responsable del artículo.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Los autores agradecen al Dr. Kyle Steeland, de la Emory University, sus comentarios al trabajo.
Esta técnica usa una constante de suavizamiento: si la constante es cercana a 1 equivale a que dicha constante afecta mucho más al nuevo pronóstico, y al contrario, cuando dicha constante es cercana a 0 el nuevo pronóstico será muy parecido a la observación más antigua. Si se desea una respuesta rápida a los cambios de la variable se debe elegir una constante de suavizamiento mayor. La fórmula que relaciona el coeficiente y la serie de tiempo viene dada por St[2]=αSt+(1−α)St−1[2], donde St=αxt+(1−α)St−1. Para generar dicho suavizamiento es necesario conocer los valores S0 y St , y xt corresponde a los valores de la serie original31,36.
La función de densidad de probabilidad para la función gamma generalizada viene dada por f(y;κ,μ,σ)=(γγ/(σyγΓ(γ)))e(zγ−u);y≥0, en donde γ=|κ|−2,z=sign(κ)×{(ln(y)−μ)/σ} y u=γexp(|κ|z). El parámetro μ es igual a xtβ, donde x es la matriz de predictores que incluye al intercepto y β es el vector de coeficientes. Para la distribución generalizada Gamma, el valor esperado condicional en x viene dado por. E(y/x)=exp[xβˆ+(σˆ/κˆ)ln(κˆ2)+ln(Γ{(1/κˆ2)+(σˆ/κˆ)}−ln(Γ(1/κˆ2))], donde σˆ tiene la siguiente expresión σˆ=(1/n)∑iexp(α0+α1ln(f(xi))), si ln(σ) es parametrizado como α0+α1ln(f(x)).
Puesto que se requiere expresar las estimaciones y los resultados en la escala original de medición, se trabaja con la exponenciación del modelo usando la transformación log-gamma μ=E(Y)=exp(xtβ), y así aseguramos que la transformación no afecte a las interpretaciones en lo que se refiere directamente a la escala de medida original28.
1) Modelo para un predictor
La metodología MARS propuesta por Friedman29 selecciona K nodos de la variable predictora x, denotados por tk , k=1,.......,K, los cuales podrían corresponder a cada una de las observaciones de la variable, y luego se definen K+1 regiones sobre el rango de x, en donde se asocia a cada nodo la función de suavizamiento lineal, generando una familia de funciones base de la forma:
en donde (x−tk)+q se conoce como función de truncamiento. Para la aproximación de orden q se estima la función fˆq(x)=∑K=0K+qakBK(q)(x); generalmente, el orden de suavizamiento que se tome debe ser ≤3, para que la función y sus q−1 derivadas sean continuas. Esta restricción y el uso de polinomios en cada subregión producen funciones suavizadas y ajustadas.2) Generalización con p predictores
Para el vector de predictores x=(x1,x2,…,xp), la función de suavizamiento se define de forma análoga al caso univariado. En este caso, el espacio Rp se divide en un conjunto de regiones disjuntas y dentro de cada región se ajusta un polinomio de p variables.
Para p>2 se consideran regiones disjuntas que definen la aproximación de suavizamiento como productos tensores de intervalos disjuntos en cada una de las variables delineadas por la ubicación del nodo. Así, ubicando Kj nodos en cada variable produce un producto de Kj+1 regiones, j=1,…,p.
Un conjunto de funciones base que generan el espacio de las funciones de suavizamiento sobre todo el conjunto de regiones es el producto tensorial de las correspondientes basales de suavizamiento unidimensionales asociadas con la ubicación de los nodos en cada variable dada por:
La selección de las funciones base consiste en elegir un buen conjunto de regiones para definir la aproximación de suavizamiento adecuada al problema; MARS genera funciones base mediante un proceso de tipo paso a paso. Se inicia con una constante en el modelo y luego comienza la búsqueda de una combinación variable-nodo que mejora el modelo. La mejora se mide en parte por el cambio en la suma de errores cuadráticos (MSE). Se agregan sucesivamente funciones base para reducir el MSE.
Con objeto de evaluar este modelo, Friedman propone usar el estadístico Generalized Cross Validation,
con C(M)=1+traza(B(BtB)−1Bt) , donde B es la matriz de diseño, el numerador es la falta de ajuste sobre los datos de entrenamiento y el denominador es un término penalizado que refleja la complejidad del modelo.