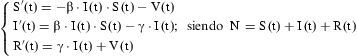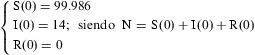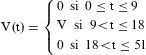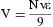La utilización conjunta de árboles de decisión y modelos epidemiológicos basados en ecuaciones diferenciales es un método apropiado para la evaluación económica de medidas profilácticas ante enfermedades infecciosas. Estos modelos permiten combinar el comportamiento dinámico de la enfermedad con el consumo de recursos sanitarios. Para ilustrar este tipo de modelos se ajusta un sistema dinámico de ecuaciones diferenciales al comportamiento epidémico de la gripe en España, con el fin de proyectar el impacto epidemiológico de la vacunación antigripal. Los resultados del modelo dinámico se implementan en un diagrama con estructura de árbol para medir el consumo de recursos sanitarios y su repercusión en términos monetarios.
The joint utilization of both decision trees and epidemiological models based on differential equations is an appropriate method for the economic evaluation of preventative interventions applied to infectious diseases. These models can combine the dynamic pattern of the disease together with health resource consumption. To illustrate this type of model, we adjusted a dynamic system of differential equations to the epidemic behavior of influenza in Spain, with a view to projecting the epidemiologic impact of influenza vaccination. The results of the epidemic model are implemented in a diagram with the structure of a decision tree so that health resource consumption and the economic implications can be calculated.
Los modelos matemáticos dirigidos a obtener proyecciones sobre las consecuencias de adoptar una intervención sanitaria son la base de la mayoría de los estudios de evaluación económica. Los instrumentos más empleados en la literatura son los árboles de decisiones y las cadenas de Markov1, aunque recientemente también se están empleando modelos de simulación de eventos discretos. La ventaja de este tipo de instrumentos estriba en su sencillez, pero tienen el inconveniente de que consideran que la fuerza de la infección (tasa de infección por cada individuo susceptible) se mantiene constante a lo largo del período estudiado, y por ello no tienen en cuenta una parte del efecto que pueden generar ciertas medidas profilácticas como la vacunación2. En realidad, la fuerza de la infección depende del número de individuos infectivos que hay en cada momento. La alternativa válida consiste en utilizar, en la evaluación económica, los modelos dinámicos desarrollados por los epidemiólogos para representar epidemias como las de peste y gripe. Su utilización permite captar tanto el efecto directo derivado de la reducción del número de susceptibles como el indirecto (efecto rebaño) asociado a la disminución del número de contactos entre susceptibles e infectivos. Sin embargo, en la literatura científica española son escasas las evaluaciones económicas basadas en modelos dinámicos. El motivo es la dificultad metodológica que plantean las ecuaciones diferenciales, que son la herramienta matemática en que se basan.
Los árboles de decisiones y los modelos dinámicos se pueden utilizar de forma complementaria para representar la decisión a tomar. Si se adopta una perspectiva sanitaria para realizar el estudio, una vez reproducidos los efectos epidemiológicos se está en condiciones de medir sus consecuencias en el consumo de recursos sanitarios; para ello se incluyen los resultados obtenidos con el modelo dinámico en un diagrama con estructura de árbol. De este modo, el modelo global tiene un carácter mixto: un enfoque dinámico para el modelado del comportamiento epidemiológico de la enfermedad combinado con otro en forma de árbol de decisión para medir las consecuencias en el consumo de recursos sanitarios y de otra índole.
El objetivo de este trabajo es presentar de forma guiada la construcción de un modelo dinámico, cuyo funcionamiento y resultados se ilustrarán mediante una aplicación a la evaluación económica de la vacunación antigripal en España.
Material y métodosPara mostrar el desarrollo de los modelos dinámicos se van a utilizar datos referentes al contexto de la vacunación antigripal de población sana en edad laboral, en España, para una hipotética cohorte de 100.000 individuos. A partir de la situación de 1 año epidemiológico, la cadena de contagio susceptible, infectivo y resistente (SIR) se adapta correctamente al comportamiento epidémico de la gripe3. La población quedará dividida en 3 clases de individuos: los susceptibles (que están en condiciones de ser contagiados), los infectivos (aquellos que infectan o pueden infectar a los susceptibles) y los resistentes (los que presentan resistencia al agente infeccioso al recuperarse de la enfermedad—inmunización natural— o al quedar inmunizados por un programa de inmunización —inducida o artificial—).
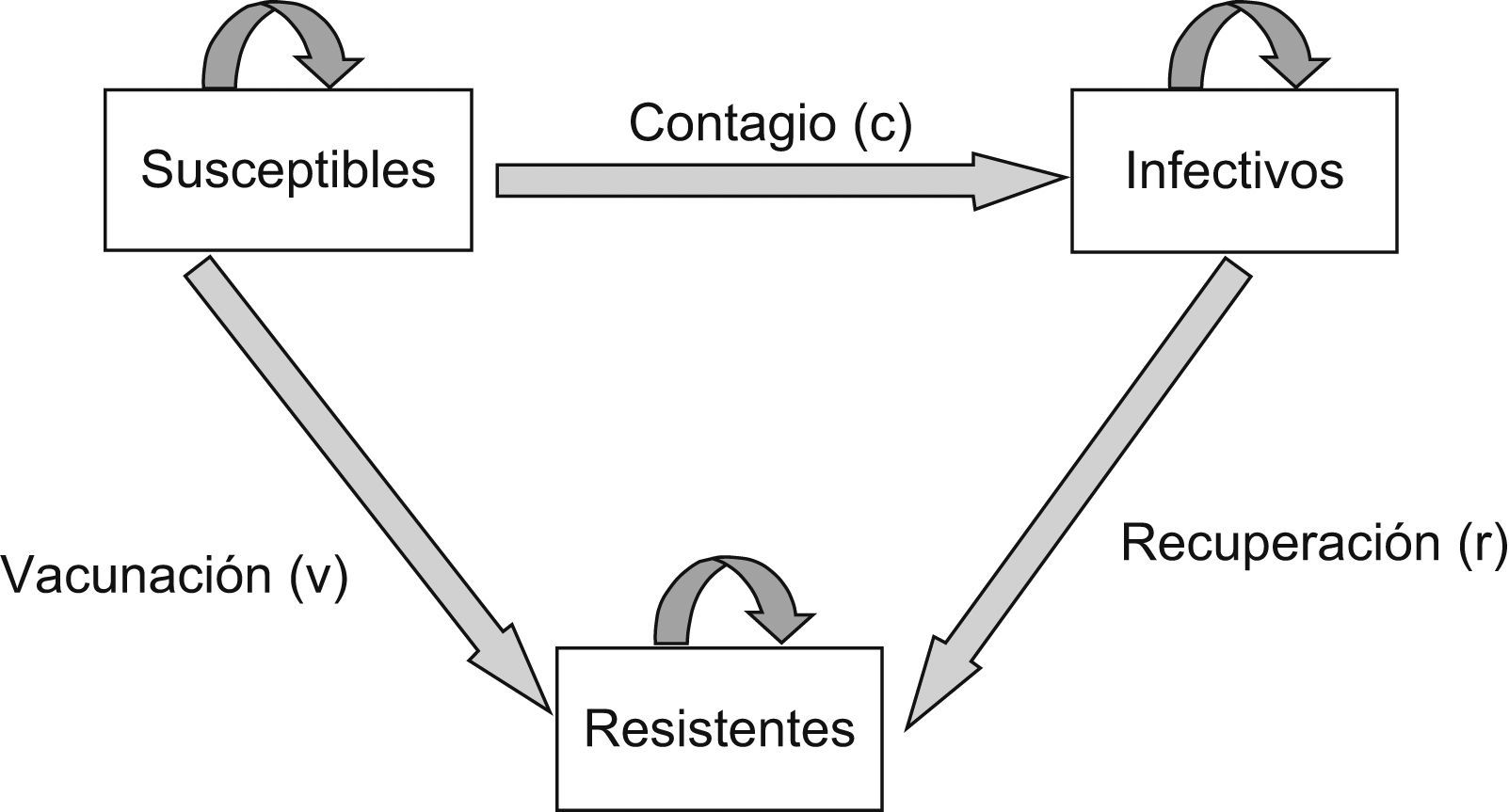
En la práctica se emplean dos enfoques alternativos a la hora de dar forma a este patrón epidemiológico: el estático y el dinámico. En el enfoque estático se pueden emplear cadenas de Markov. La figura 1 muestra la cadena correspondiente al patrón epidemiológico propuesto en el ejemplo. Para que genere resultados, se necesita conocer las probabilidades de transición entre los diversos estados (c, r y v) y las probabilidades de permanecer en el mismo estado de salud cada ciclo, es decir, cada semana para el caso estudiado. La probabilidad de vacunación sería nula si el modelo no actuase durante el período de vacunación, entre las semanas 9 y 18. El inconveniente de este tipo de modelo es que no tiene en cuenta los contactos que se producen entre los individuos susceptibles y los infectivos.
Si, por el contrario, se adoptase el enfoque dinámico, se cuenta con 2 instrumentos para estudiar analíticamente la evolución epidémica de una enfermedad infecciosa: ecuaciones en diferencias finitas y ecuaciones diferenciales4–6. La utilización de las primeras es más sencilla, ya que consideran el tiempo como una variable discreta y permiten dejar el campo del cálculo infinitesimal al margen, y se pueden realizar con programas de fácil manejo como EXCEL, pero tienen el inconveniente de que la consideración de la variable temporal no se ajusta a la realidad, pues el tiempo es una variable continua. Las ecuaciones diferenciales consideran el tiempo como una variable continua, pero requieren programas informáticos de mayor complejidad matemática, como Mathematica o Derive. Con estos instrumentos se da entrada a los contactos entre infectivos y susceptibles multiplicando sus cifras en cada momento de tiempo considerado [I (t)·S (t)] según el siguiente sistema no lineal de ecuaciones diferenciales ordinarias:
donde t es el momento de tiempo medido en semanas; N el tamaño de la población considerada; S(t), I(t) y R(t) el número de susceptibles, infectivos y resistentes en cada momento de tiempo t, respectivamente; β el coeficiente de transmisión; y γ el coeficiente de retiro natural, es decir, es un indicador del ritmo con que los individuos contagiados dejan de ser infectivos. Las derivadas respecto a t de primer orden, S′(t), I′(t) y R′(t), indican las tasas de variación instantánea en el tiempo de las variables asociadas a las clases consideradas (susceptibles, infectivos y resistentes).Este sistema lo idearon Kermack y McKendrick7, y con él consiguieron una buena réplica de las cifras poblacionales asociadas a una epidemia de peste en Bombay (1905–1906). Anderson y May8,9 comenzaron a emplearlo de forma regular a partir de la década de 1970 y lo adaptaron a varias enfermedades infecciosas; en 199910 lo propusieron para el estudio de la gripe. De hecho, este mismo modelo ha sido retomado para la gripe en diversos estudios de carácter epidemiológico11–15.
La resolución de este sistema requiere la distribución inicial de la población, es decir, los números iniciales de susceptibles, infectivos y resistentes, el coeficiente de retiro, y el de transmisión. La obtención de los valores anteriores implica tener claro el período temporal de referencia (semana, mes, año…), o con otras palabras, la unidad de tiempo aplicable durante el período estudiado. En este ejemplo, el período será la semana durante el año epidemiológico. Los coeficientes del modelo se estiman aplicando un procedimiento de aproximaciones sucesivas detallado seguidamente.
El coeficiente de retiro natural (γ) depende del período de tiempo en que un individuo contagiado con gripe presenta la máxima infectividad, según Anderson y May10 en torno a 3 días (3–7 semanas). En España, el valor que reproduce satisfactoriamente el perfil de la onda epidémica respetando las cifras de incidencia notificada al Centro Nacional de Epidemiología16 es 2,02 días (2,02-7 semanas), por lo que γ=17=3,47.Elcoeficientedetransmisio´n(β=3,4796.015) es el indicador de la contagiosidad del virus, depende del anterior y del número de susceptibles en el auge de la onda epidémica (96.015 individuos), que se ha obtenido reduciendo proporcionalmente la cifra en la población española para ajustar el comportamiento del modelo a un colectivo de 100.000 individuos. Se ha escogido este tamaño poblacional (N) por ser un valor empleado con frecuencia en las fuentes de información epidemiológica, y además porque facilita la interpretación y el cálculo de los indicadores económicos del estudio. Para enfermedades con un período epidemiológico más prolongado, en las que resulta difícil estimar el número de susceptibles en el auge de la onda epidémica, se emplea el concepto de número reproductivo básico [ρ (0)], que es el número medio de contagios que puede generar un individuo infectivo al comienzo del período epidemiológico, en la sociedad de referencia. Junto con el número de susceptibles al inicio del período estudiado[S(0)]aplicarı´amoslasiguientefo´rmula:β=ρ(0)γS(0).
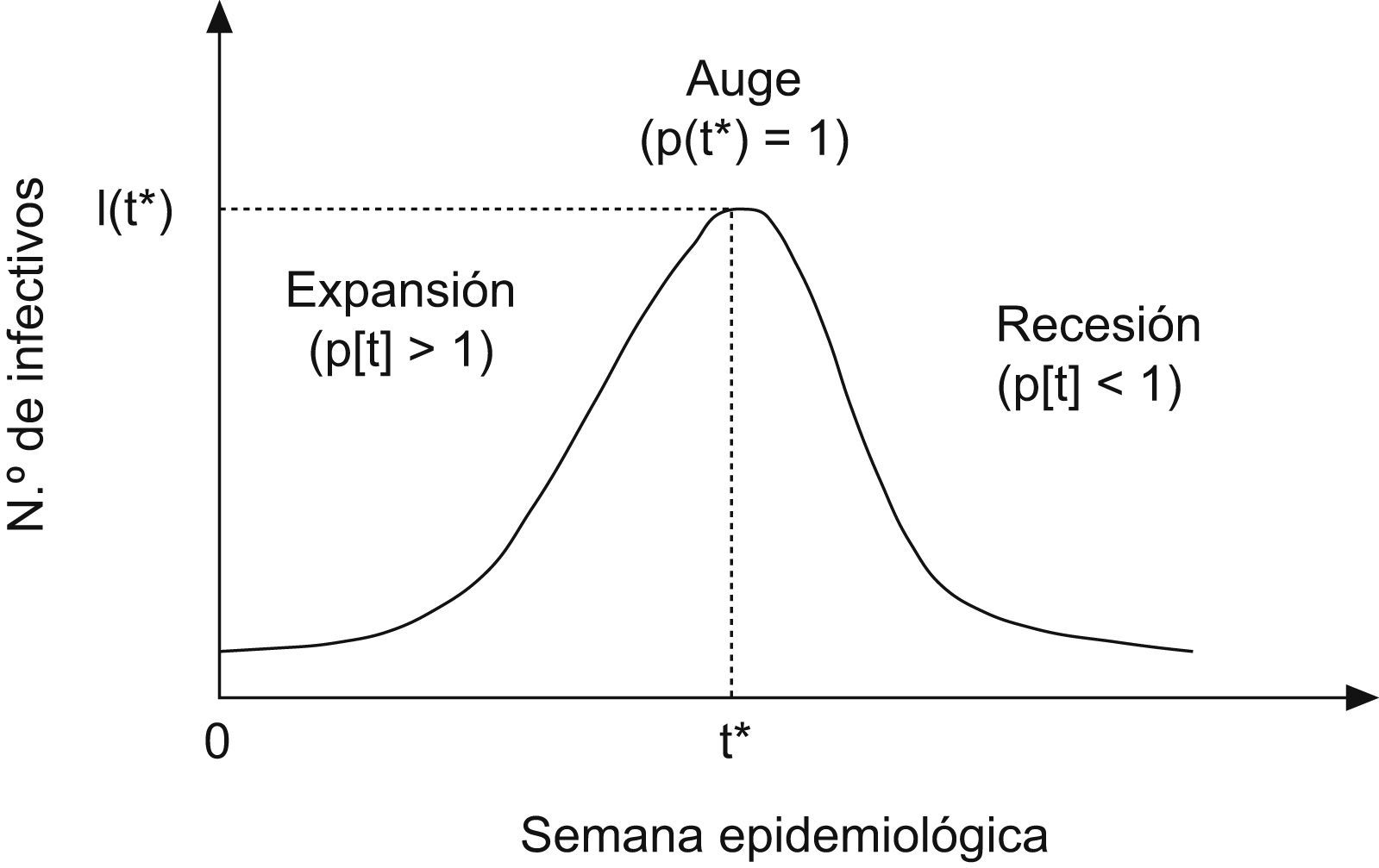
La figura 2 muestra la relación existente entre el valor del número reproductivo y la evolución de la onda epidemiológica.
Según la distribución por clases de la población en la primera semana del período epidemiológico estudiado (semana 0), los valores iniciales para la resolución del sistema de ecuaciones diferenciales son los siguientes:
El número de infectivos en la primera semana, I(0)=14, es un valor promedio basado en series históricas de la enfermedad, cedidas por el Centro Nacional de Epidemiología.
Para definir la forma de la función de vacunación V(t) se ha recogido el efecto de la vacunación reduciendo el número de susceptibles según el número de individuos vacunados eficazmente, es decir, aquellos vacunados a quienes ha hecho efecto la vacuna según su eficacia. Se trata de incluir la vacunación de forma paulatina con una función definida por intervalos con la forma siguiente:
donde V es el hipotético número de individuos vacunados semanalmente, el tiempo está medido en semanas y el período epidemiológico de estudio es el año epidemiológico de la gripe (52 semanas). Siguiendo las recomendaciones del Centro Nacional de Epidemiología para esta enfermedad, se considera año epidemiológico desde la semana 33 (tercera semana de agosto) hasta la 32 (segunda semana de agosto del año siguiente)17.Se puede apreciar que el intervalo en que no es nula V (t) no coincide con el asociado a la campaña de vacunación (octubre y noviembre), sino que está diferido 2 semanas, que es el tiempo medio que tarda la vacuna en producir la inmunidad del individuo vacunado18,19. El cálculo del hipotético número de individuos vacunados cada semana se efectúa del siguiente modo:
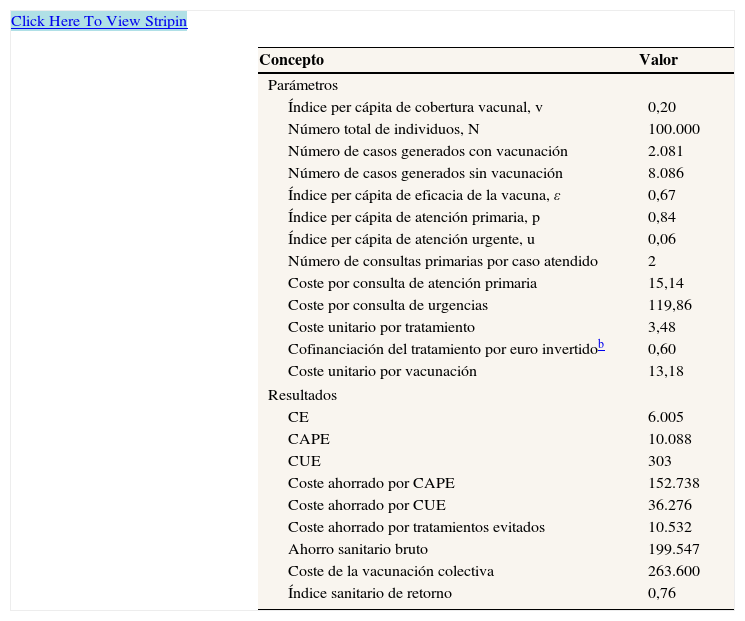
donde N es el tamaño de la población diana; v el índice per cápita de vacunación (cobertura vacunal) alcanzado en la campaña de vacunación; ε el índice per cápita de eficacia de la vacuna; y 9 la duración aproximada de la campaña de vacunación en semanas. En la figura 3 se observa cómo incide la vacunación en la población. Realmente la vacunación actúa haciendo que parte de los individuos que eran susceptibles pasen a ser resistentes, y con ello se reduce la posibilidad de contagio al decaer el número de contactos entre susceptibles e infectivos.Para la resolución del sistema de ecuaciones diferenciales se ha empleado un método de Runge-Kutta de cuarto orden por ser bastante preciso20,21. El resto de los parámetros que requiere el estudio se presentan en la tabla 1 y se han obtenido de estudios publicados anteriormente referidos al ámbito español22,23. Los valores monetarios están calculados en euros del año 2008.
Valores de parámetros y resultadosa
| Concepto | Valor |
| Parámetros | |
| Índice per cápita de cobertura vacunal, v | 0,20 |
| Número total de individuos, N | 100.000 |
| Número de casos generados con vacunación | 2.081 |
| Número de casos generados sin vacunación | 8.086 |
| Índice per cápita de eficacia de la vacuna, ε | 0,67 |
| Índice per cápita de atención primaria, p | 0,84 |
| Índice per cápita de atención urgente, u | 0,06 |
| Número de consultas primarias por caso atendido | 2 |
| Coste por consulta de atención primaria | 15,14 |
| Coste por consulta de urgencias | 119,86 |
| Coste unitario por tratamiento | 3,48 |
| Cofinanciación del tratamiento por euro invertidob | 0,60 |
| Coste unitario por vacunación | 13,18 |
| Resultados | |
| CE | 6.005 |
| CAPE | 10.088 |
| CUE | 303 |
| Coste ahorrado por CAPE | 152.738 |
| Coste ahorrado por CUE | 36.276 |
| Coste ahorrado por tratamientos evitados | 10.532 |
| Ahorro sanitario bruto | 199.547 |
| Coste de la vacunación colectiva | 263.600 |
| Índice sanitario de retorno | 0,76 |
CAPE: consultas de atención primaria evitadas; CE: casos evitados; CUE: consultas de urgencias evitadas.
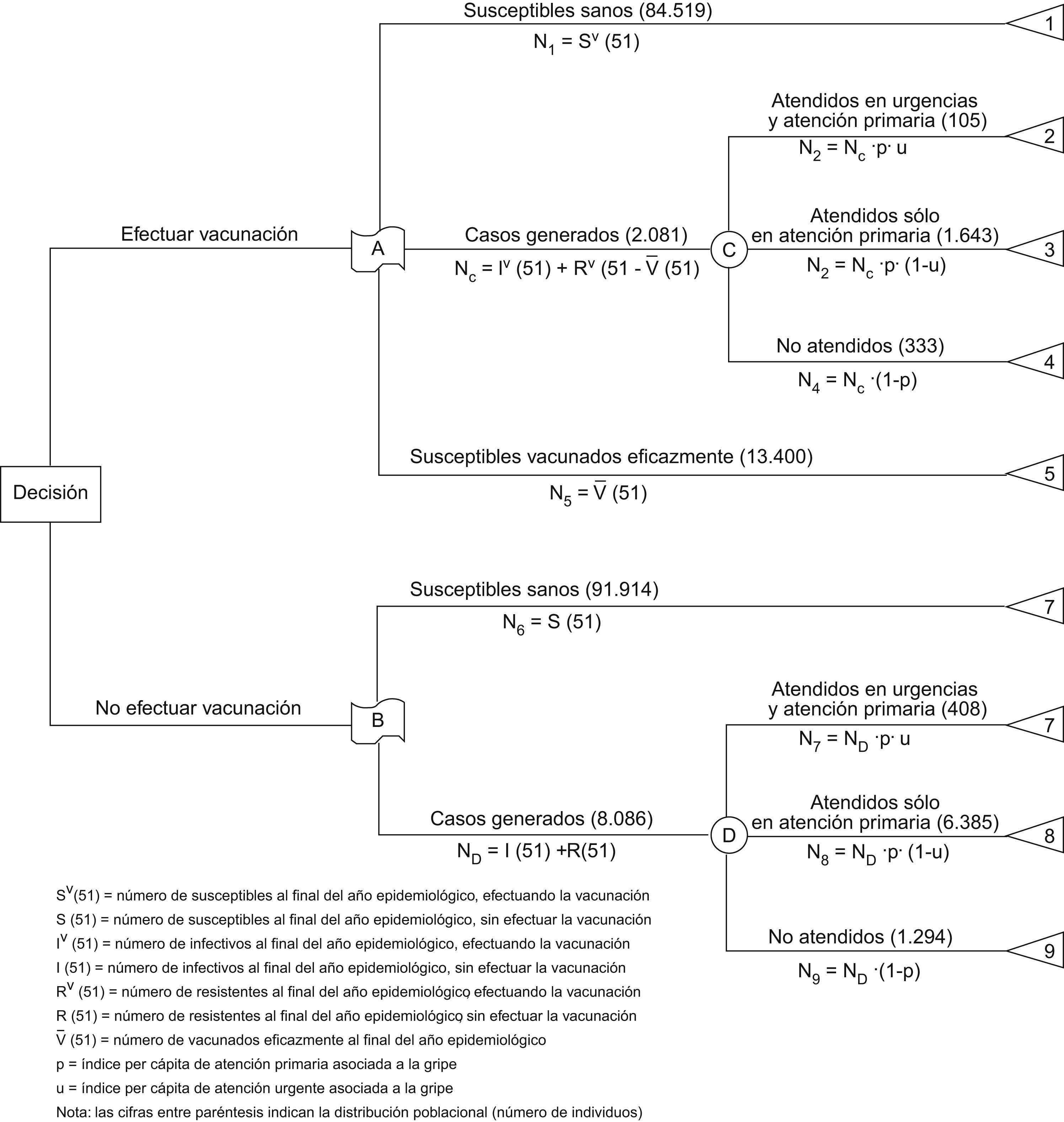
La repercusión en el grado de utilización de los recursos sanitarios queda plasmada en un árbol compuesto por 3 tipos de vértices: deterministas, dinámicos y aleatorios. Los vértices deterministas, representados con cuadrados o rectángulos, están asociados a las decisiones alternativas que puede adoptar el gestor en un momento concreto. Los vértices dinámicos, representados con rectángulos mixtilíneos ondulados, simbolizan el modelo dinámico de transmisión (SIR) que reproduce el efecto epidemiológico de la decisión adoptada. Y finalmente, los vértices aleatorios, representados con círculos, están asociados a acontecimientos que escapan del control del gestor, y por ello las aristas que parten de ellos tienen asociadas probabilidades (frecuencias relativas esperadas) estimadas mediante frecuencias relativas observadas de los índices de atención primaria y urgente asociados a la enfermedad.
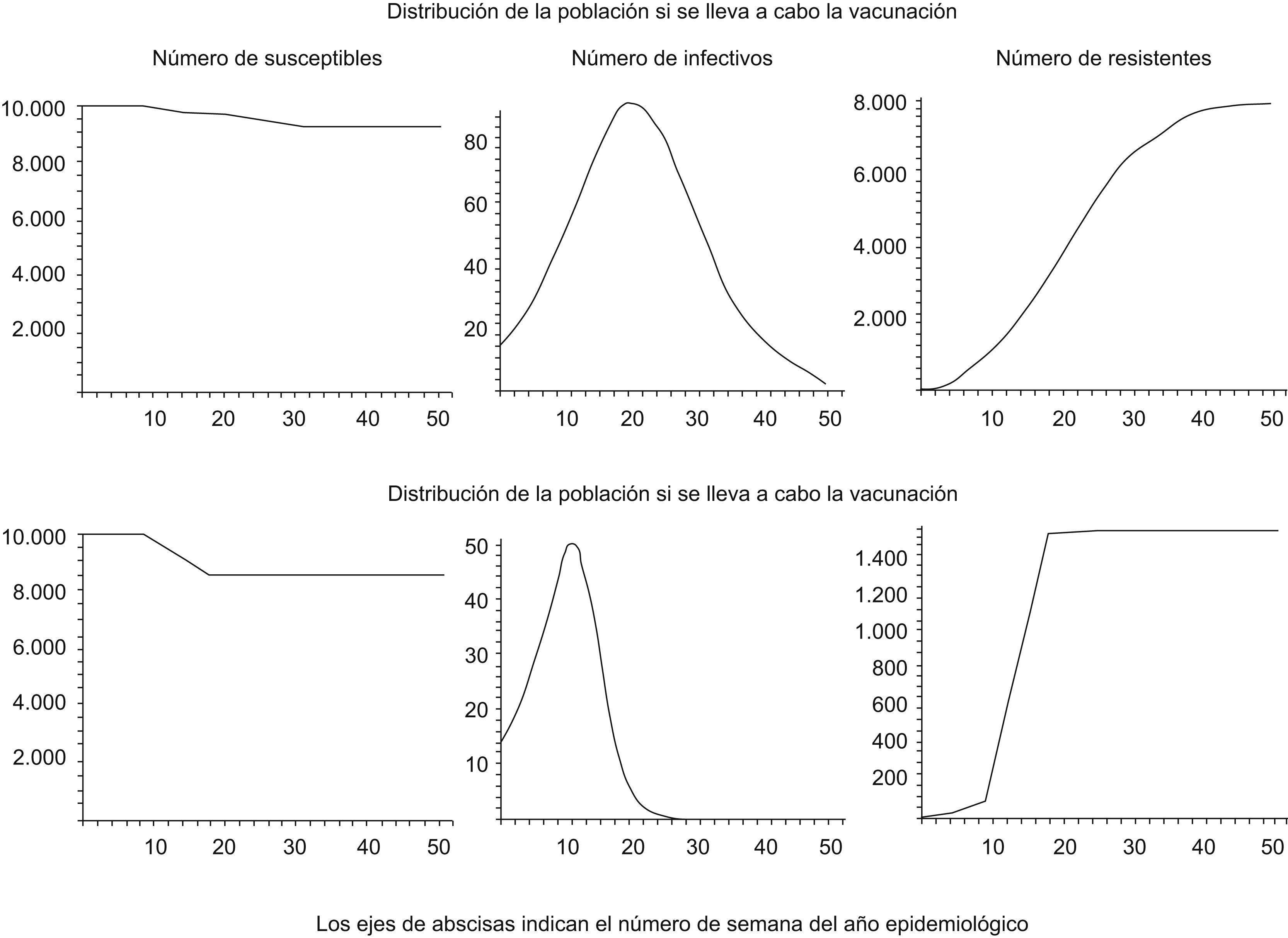
ResultadosEn la figura 4 aparecen las curvas solución del modelo dinámico que reproduce el comportamiento epidémico de la gripe. Se trata de una forma sintética de presentar los resultados. No obstante, el programa informático Mathematica también ofrece estos resultados en forma de tabla. Tomando los valores basales de cobertura (20%) y eficacia (67%), resulta una vacunación semanal aproximada de 1.489 individuos. El modelo dinámico reproduce el comportamiento epidémico de la gripe considerando una población de 100.000 individuos y la cobertura eficaz (13.400 individuos vacunados). Al comparar los 2 paneles de la figura 4, se puede comprobar que cuando se lleva a cabo la vacunación (panel B), a partir de la novena semana se produce una disminución más pronunciada del número de susceptibles, que coincide con un aumento, en los mismos términos, del número de resistentes; la onda epidémica (número de infectivos) es menos intensa cuando se ha llevado a cabo la vacunación.
La repercusión en el grado de utilización de los recursos sanitarios queda plasmada en el árbol de decisión de la figura 5. Con los resultados indicados por este diagrama y los valores de los parámetros monetarios se calcula la efectividad de la medida en términos monetarios. En la tabla 1 se presentan diferentes medidas de la efectividad alcanzada con la intervención preventiva. Desde una perspectiva sanitaria, el efecto económico de la intervención queda patente comparando el coste de la vacunación con el ahorro sanitario bruto derivado de la intervención. En este caso, sería una intervención ineficiente desde el punto de vista económico tradicional, puesto que el índice de retorno indica que por cada euro invertido en la vacunación sólo se ahorrarían 76 céntimos. Por otra parte, el cociente coste-efectividad resulta ser de 10,66 euros por caso evitado.
DiscusiónEl presente estudio muestra cómo implementar modelos mixtos que dan entrada a la consideración dinámica de las enfermedades infecciosas. Anteriormente, otros estudios tanto nacionales23 como internacionales24–26 han mostrado que la vacunación antigripal puede suponer importantes ahorros de recursos sanitarios. Aun así, en todos ellos han quedado subestimados estos ahorros por no emplear un enfoque dinámico para medir el impacto epidemiológico de la medida; no se ha considerado el efecto “rebaño”, propio de los programas de vacunación14.
Según los resultados de este estudio, la intervención sanitaria no resulta eficiente, en términos monetarios, pero se podría ofrecer una subvención de hasta 10 euros para su implantación sin que superase los ahorros generados por la medida profiláctica. Tampoco se puede dejar de lado la oportunidad en el tiempo de la liberación de recursos sanitarios, ya que supondría una descarga de las consultas de atención primaria y urgencias en la temporada epidémica de la gripe.
No se ha llevado a cabo un análisis de sensibilidad puesto que el objeto de este trabajo no era realizar una evaluación económica completa, sino mostrar cómo se pueden emplear este tipo de modelos y la forma de presentar los resultados obtenidos. En cualquier caso, para incluir los aspectos de incertidumbre en las evaluaciones basadas en este tipo de modelos, habría que proceder como de costumbre: elaborar análisis de sensibilidad univariados o multivariados, estimar mediante simulación y técnicas bayesianas, etc.
Las series temporales que generan los modelos dinámicos son de especial interés para la administración sanitaria, puesto que basándose en ellas se pueden tomar decisiones para una mejor planificación de la utilización de los recursos sanitarios. Un posterior análisis cualitativo (llamando así al análisis matemático de las condiciones que se deben dar para que el modelo genere ciertos resultados) de los modelos dinámicos aplicados en enfermedades infecciosas para las que exista vacuna permitiría conocer cuántos individuos deberían ser vacunados para conseguir que la onda epidémica alcanzase la fase recesiva. La generación de casos de gripe cada temporada es algo inevitable, puesto que una serie de casos se generan antes de la campaña de vacunación, no se puede vacunar a toda la población y la vacuna no resulta eficaz en todos los casos. Ante una posible pandemia de gripe aviar, el modelo epidemiológico propuesto permite reproducir la potencial onda pandémica a partir de la incidencia media prevista, o plantear distintos escenarios pandémicos según la experiencia histórica acumulada de pandemias anteriores y las posibles medidas profilácticas disponibles en cada momento. El Centro Nacional de Epidemiología dispone de información de esta naturaleza, ya que en España la gripe fue una de las primeras enfermedades respiratorias sujeta a vigilancia al quedar incluida en la lista de enfermedades de declaración obligatoria en 190427.
El análisis de coste-efectividad de la vacuna del virus del papiloma humano (VPH) es otro ejemplo de estudio que requiere el uso de modelos dinámicos28. Sin embargo, la revisión de la literatura muestra que los autores han usado tanto estudios llevados a cabo con modelos de Markov29,30 como con modelos dinámicos31,32. Teniendo en cuenta que el VPH es contagioso, la vacunación tiene efecto no sólo en las personas vacunadas sino también en las no vacunadas, ya que su riesgo de contagio disminuye como consecuencia de la disminución de la población infectiva. Los modelos de Markov no permiten incorporar este aspecto de forma directa en la medida de resultados, por lo que infravaloran la efectividad de la intervención. Las dificultades que supone construir y resolver un sistema de ecuaciones diferenciales pueden resolverse incorporando al equipo de investigación matemáticos con experiencia en el tema. Quizás el problema radique en que las enfermedades infecciosas se han visto como un problema de salud resuelto, por lo que los métodos para su estudio han dejado de tener interés para las autoridades sanitarias y para los investigadores. Sin embargo, el final del siglo xx supuso la aparición de nuevos problemas de salud de tipo infectocontagioso. Valdría la pena que los grupos españoles de investigación en evaluación económica utilizaran métodos como los sistemas dinámicos basados en ecuaciones diferenciales, para que las nuevas intervenciones dirigidas a estos problemas se evaluasen con mayor precisión.